I Problemi della prof
Difficoltà: Alta
Capitolo 14 - Equazioni di Maxwell e onde elettromagnetiche Problema 14.12.1
a) Determinare la frequenza massima dello spettro continuo di un tubo a raggi X operante a 30.000V. b) Calcolare la minima lunghezza d’onda di un raggio X prodotto da un generatore di Van der Graaf, operante a 50.000V. […]
Capitolo 14 - Equazioni di Maxwell e onde elettromagnetiche Problema 14.12.2
La potenza elettrica sviluppata in un tubo a raggi X percorso da una corrente di intensità i=10mA è P=2,0KW. a) Qual è la d.d.p. applicata al tubo? b) Qual è l’energia massima degli elettroni che colpiscono l’anticatodo? c) Qual è la lunghezza d’onda minima dei raggi X emessi? […]
Capitolo 14 - Equazioni di Maxwell e onde elettromagnetiche Problema 14.12.3
a) Calcolare la frequenza massima dei raggi X prodotti dall’urto di elettroni accelerati da una d.d.p. di 80.000V sull’anticatodo. b) Calcolare lo spessore di piombo necessario per ridurre ad un quarto l’intensità della radiazione uscente, sapendo che il coefficiente di assorbimento del piombo per tale radiazione è […]
Capitolo 14 - Equazioni di Maxwell e onde elettromagnetiche Problema 14.12.4
Un fascio di raggi X è diffratto da un cristallo di salgemma. Lo spettro di primo ordine corrisponde ad un angolo di 6,8° e la distanza fra i piani è 2,81.10-10m. Determinare la lunghezza d’onda dei raggi X e la posizione del secondo ordine. […]
Capitolo 14 - Equazioni di Maxwell e onde elettromagnetiche Problema 14.12.5
Un fascio di raggi X di lunghezza d’onda λ =5.10-11m incide su una polvere composta da cristalli microscopici di KCl orientati a caso. La costante reticolare nel cristallo è 3,14.10-10m. […]
Capitolo 14 - Equazioni di Maxwell e onde elettromagnetiche Problema 14.12.6
Lo ioduro di potassio KI è un cristallo cubico avente densità 3,13g/cm3. a) Trovare la minima distanza tra i piani, cioè il lato di una cella elementare. b) Determinare gli angoli corrispondenti ale prime due riflessioni di Bragg per raggi X di lunghezza d’onda 3,0. […]
Capitolo 14 - Equazioni di Maxwell e onde elettromagnetiche Problema 14.2.2
(Extracorrente di chiusura e di apertura di un circuito)
In un circuito di resistenza R=10Ω e induttanza L=1,0H è inserito un generatore di f.e.m. costante fp=25V (fig.14.8).
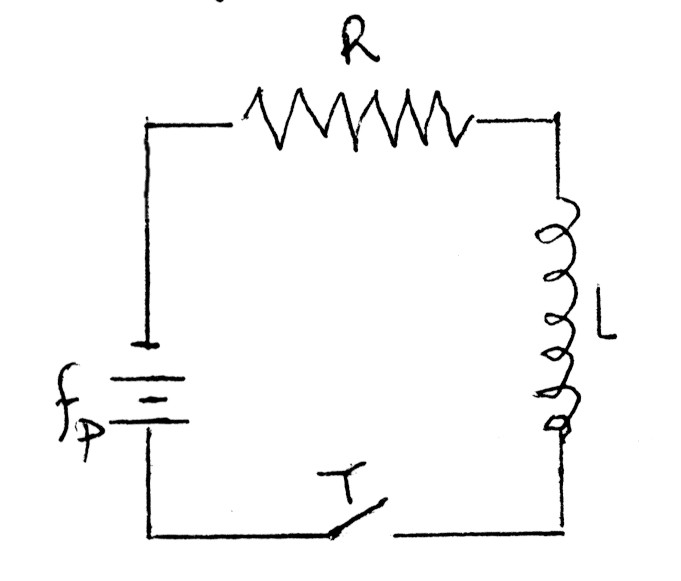fig.14.8
a) Calcolare il valore dell’intensità di corrente dopo un tempo t=0,2s dalla sua chiusura. […]
Capitolo 14 - Equazioni di Maxwell e onde elettromagnetiche Problema 14.2.3
Una induttanza L=1,5H è in serie ad una resistenza R=2,0Ω e ad una batteria di f.e.m. f =1,0V. Calcolare: a) qual è il valore della d.d.p. ai capi di R, dopo un tempo t1=1,2s dalla chiusura del circuito; […]
Capitolo 14 - Equazioni di Maxwell e onde elettromagnetiche Problema 14.2.4
Un condensatore di capacità C=2,0μ F viene caricato attraverso una resistenza R=0,10MΩ da una batteria di f.e.m. f=100V. a) Dopo quanto tempo dalla chiusura del circuito la d.d.p. ai capi del condensatore è V1=50V? b) Quanto vale la corrente che passa nello stesso istante attraverso R e quanto vale la d.d.p. […]
Capitolo 14 - Equazioni di Maxwell e onde elettromagnetiche Problema 14.2.5
Un condensatore di capacità C=9,0pF è caricato ad una d.d.p.V0=300V e viene chiuso su una resistenza R=105Ω. a) Dopo quanto tempo il suo potenziale è sceso a V1=100V? b) Quanto vale in quell’istante la d.d.p. […]
Capitolo 14 - Equazioni di Maxwell e onde elettromagnetiche Problema 14.3.1
Si vuole che il circuito oscillante di fig.14.11 abbia una frequenza ν=104Hz. Se è C=10-10F, che valore deve avere l’induttanza L? Sapendo che l’energia del circuito è E=1,27.10-2J, […]
Capitolo 14 - Equazioni di Maxwell e onde elettromagnetiche Problema 14.4.1
Nel circuito di fig.14.16 alimentato da una f.e.m. alternata f=Fsenωt, con F=120V e frequenza ν=50Hz, sono inseriti in serie un condensatore di capacità C=1,0μF e una induttanza L=2,4H.
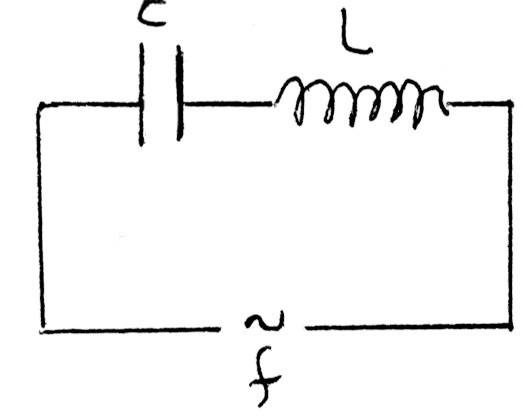fig.14.16
La resistenza del circuito è trascurabile. Calcolare:
a) l’intensità di corrente massima I erogata dal generatore; […]