I Problemi della prof
Capitolo 14 - Equazioni di Maxwell e onde elettromagnetiche Problema 14.11.1
Entro quali limiti varia l’angolo di Brewster per l’intervallo di lunghezze d’onda che vanno da 4000A° a 8000A°, se il materiale su cui la luce incide è vetro, il cui indice di rifrazione n varia da n1=1,51 a n2=1,53? […]
Capitolo 14 - Equazioni di Maxwell e onde elettromagnetiche Problema 14.11.2
L’angolo limite per la luce in una certa sostanza è di 45°. Quanto vale l’angolo di Brewster per la stessa sostanza? […]
Capitolo 14 - Equazioni di Maxwell e onde elettromagnetiche Problema 14.11.3
Un raggio polarizzato linearmente incide normalmente su un cristallo birifrangente in maniera che il piano di vibrazione forma un angolo α=30° con l’asse del cristallo. Indicando con I l’intensità del raggio incidente, qual è il rapporto rispetto ad I delle intensità […]
Capitolo 14 - Equazioni di Maxwell e onde elettromagnetiche Problema 14.11.4
Un fascio di luce polarizzata linearmente incide perpendicolarmente su di una lastra di calcite (con le facce parallele all’asse ottico) con il vettore elettrico formante un angolo di 60° con l’asse ottico. Trovare il rapporto delle ampiezze e delle intensità dei fasci ordinario e straordinario. […]
Capitolo 14 - Equazioni di Maxwell e onde elettromagnetiche Problema 14.11.5
a) Un raggio di luce monocromatica incide su un nicol (vedi fig.14.34).
Determinare l’angolo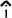 
massimo col quale la luce può incidere in modo che il raggio ordinario sia ancora totalmente riflesso dal balsamo del Canadà. Gli indici di rifrazione sono n0=1,65 e nb=1,55, […]
Capitolo 14 - Equazioni di Maxwell e onde elettromagnetiche Problema 14.11.6
Un raggio di luce polarizzata linearmente, di intensità I0, incide su di un nicol in modo che il piano di vibrazione formi un angolo α=40° con la direzione di trasmissione del nicol. Il raggio che esce ha un’intensità […]
Capitolo 14 - Equazioni di Maxwell e onde elettromagnetiche Problema 14.11.7
Un certo cristallo rifrangente ha indice di rifrazione 1,5442 e 1,5563 per le onde straordinarie e ordinarie rispettivamente, ad una lunghezza d’onda λ=600nm. a) Si calcoli il minimo spessore di cristallo necessario per produrre una differenza di cammino ottico di un quarto di lunghezza d’onda fra le onde S e O che lo attraversano. […]
Capitolo 14 - Equazioni di Maxwell e onde elettromagnetiche Problema 14.11.8
Trovare lo spessore della lamina di calcite necessaria per produrre una differenza di cammino di a) λ/4, b) λ/2, c) λ, fra il raggio ordinario e lo straordinario, con una lunghezza d’onda λ=6562A°. Gli indici di rifrazione sono rispettivamente n0=1,4846 e nS=1,6543. […]
Capitolo 14 - Equazioni di Maxwell e onde elettromagnetiche Problema 14.11.9
Fra due nicol, i cui assi di trasmissione coincidono, si pone una lamina di quarzo con le facce normali all’asse ottico, di spessore t=0,3cm e potere rotatorio K=13°/mm per λ=7300A°. Se I1 è l’intensità del fascio monocromatico di lunghezza d’onda λ […]
Capitolo 14 - Equazioni di Maxwell e onde elettromagnetiche Problema 14.11.10
Una lamina di quarzo è mezz’onda per luce di lunghezza d’onda λ=4000A° (nel vuoto). a) Determinare lo stato di polarizzazione della luce trasmessa quando incide sul cristallo della luce linearmente polarizzata di lunghezza d’onda 8000A° il cui piano di vibrazione forma un angolo di 45°con l’asse ottico. […]
Capitolo 14 - Equazioni di Maxwell e onde elettromagnetiche Problema 14.11.11
Un raggio luminoso di luce polarizzata linearmente incide perpendicolarmente su di una lamina di quarzo di spessore incognito. Supponiamo che l’asse ottico della lamina sia parallelo alla faccia di incidenza e formi un angolo di 45° con la direzione di polarizzazione della luce incidente. […]
Capitolo 14 - Equazioni di Maxwell e onde elettromagnetiche Problema 14.11.12
Si ha una lamina a mezz’onda di calcite per λ=6500A° con indici di rifrazione del raggio ordinario n0=1,65 e di quello straordinario nS=1,48. a)Se incide su di essa un fascio di raggi paralleli polarizzato linearmente, […]