Problema 1.7.1

Il moto armonico semplice di un oscillatore è descritto dall’equazione: x(t)=A\sin(Bt+C), dove A=0{,}5\text{ m},   B=2{,}0\text{ rad}\cdot\text{s}^{-1}   e   C=0{,}6\text{ rad}.
Trovare:
a) la posizione, la velocità e l’accelerazione per t=0{,}5\text{ s};
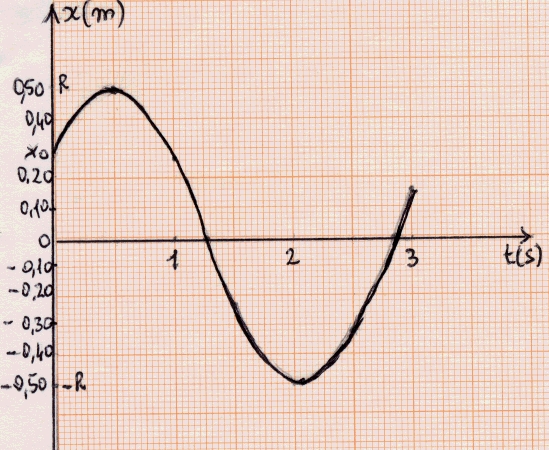
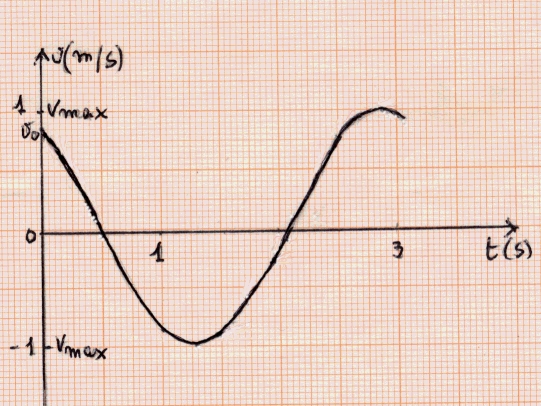
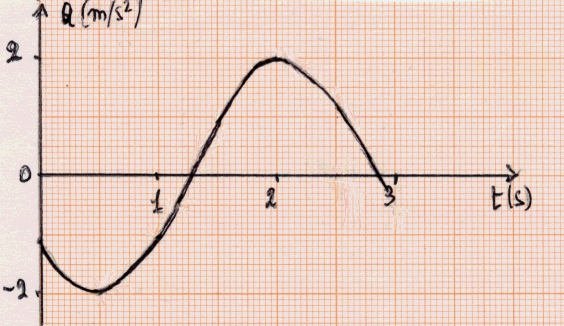
b) la rappresentazione grafica di posizione, velocità e accelerazione in funzione del tempo.

Guarda la soluzione

Ricordando l’equazione generale del moto armonico x(t)=R\sin(\omega t+\varphi_0), dove R è l’ampiezza, \omega la pulsazione e \varphi_0 la fase iniziale, si ricavano:
R=0{,}5\text{ m},   \omega=2{,}0\text{ rad/s}   e   \varphi_0=0{,}6\text{ rad}.

a) x(0{,}5)=[0{,}5\sin(1{,}6)]\text{ m}=0{,}5\text{ m};
v(t)=\omega R\cos(\omega t+\varphi_0), da cui: v(0{,}5)=[0{,}5\cdot2{,}0\cdot\cos(1{,}6)]\text{ m/s}=-0{,}030\text{ m/s}
a(t)=-\omega^2R\sin(\omega t+\varphi_0)=-\omega^2x, da cui: a(0{,}5)=-\omega^2\cdot x(0{,}5)=2{,}0\text{ m/s}^2

b) Determiniamo le condizioni iniziali (t=0):
x_0=R\sin(\varphi_0)=0{,}28\text{ m}
v_0=\omega R\cos(\varphi_0)=0{,}83\text{ m/s}
a_0=-\omega^2x_0=-1{,}1\text{ m/s}^2
Conviene ora ricavare i valori di t nei quali le funzioni s(t), v(t) e a(t) sono nulle o presentano un massimo o un minimo:

    \[ \begin{tabular}{@{}lll@{}} \toprule \multirow{3}{*}{$\sin(At+B)=0$} & $At+B=0$ & $t=-0{,}3\text{ s}$ \\ \cmidrule(l){2-3} & $At+B=\pi$ & $t=1{,}27\text{ s}$ \\ \cmidrule(l){2-3} & $At+B=2\pi$ & $t=2{,}84\text{ s}$ \\ \midrule \multirow{2}{*}{$\sin(At+B)=\pm1} & $At+B=\pi/2$ & $t=0{,}49\text{ s}$ \\ \cmidrule(l){2-3} & $At+B=3\pi/2$ & $t=2{,}06\text{ s}$ \\ \midrule [0.08 em] \end{tabular} \]

Ricordiamo che, dove  \sin(2{,}0t+0{,}6)=0, sono nulle s(t) e a(t): dove s(t) ha un massimo, a(t) ha un minimo e viceversa. Ma, se \sin(At+B)=0 allora \cos(At+B)=\pm1 e viceversa, quindi dove s(t) e a(t) hanno un massimo o un minimo lì v(t)=0 e viceversa.
Per costruire i grafici possiamo anche calcolare i valori di s(t), v(t) e a(t) per determinati valori arbitrari di t, oltre t=0 e t=0{,}5\text{ s} già calcolati. Per esempio:

    \[ \begin{tabular}{@{}cccc@{}} \toprule Tempo (s) & Spazio (m) & Velocit\`a (m/s) & Accelerazione (m/s$^2$) \\ \midrule [0.08 em] 1,0 & 0,26 & $-0{,}86$ & $-1{,}03$ \\ \midrule 1,5 & $-0{,}22$ & $-0{,}90$ & 0,89 \\ \midrule 2,0 & $-0{,}50$ & $-0{,}11$ & 2,00 \\ \midrule 2,5 & 0,32 & 0,78 & 1,26 \\ \midrule 3,0 & 0,16 & 0,95 & $-0{,}62$ \\ \midrule [0.08 em] \end{tabular}\]



Problema del Capitolo 1 - Il moto ▷ Sezione 1.7 - Moti oscillatori

Problema di difficoltà: Media