Problema 1.6.1.1
Uno sciatore percorre una tratto di pista AO, inclinato rispetto all’orizzontale di ![]() , e giunge alla sommità O della risalita con una velocità
, e giunge alla sommità O della risalita con una velocità ![]() .
.
Al di là della sommità c’è una discesa inclinata rispetto all’orizzontale di ![]() (vedi fig.1.27) e lo sciatore compie un salto, ritornando sulla pista in un punto C.
(vedi fig.1.27) e lo sciatore compie un salto, ritornando sulla pista in un punto C.
a) Descrivere la traiettoria percorsa dallo sciatore durante il salto;
b) calcolare la distanza OC;
c) calcolare la durata del salto.
(Si trascuri la resistenza dell’aria.)
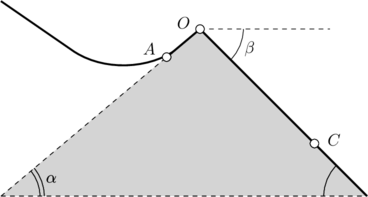
fig.1.27
a) Lo sciatore, all’inizio del salto, ha una velocità ![]() inclinata di
inclinata di ![]() rispetto all’orizzontale, con
rispetto all’orizzontale, con ![]() .
.
Prima di tutto, dobbiamo fissare un opportuno sistema di riferimento: come origine ![]() scegliamo la sommità della vetta, l’asse
scegliamo la sommità della vetta, l’asse ![]() lungo la verticale e rivolto verso l’alto e l’asse
lungo la verticale e rivolto verso l’alto e l’asse ![]() in direzione orizzontale con verso concorde al moto.
in direzione orizzontale con verso concorde al moto.
L’equazione della traiettoria (vedi il cap.1.6 – conclusioni) rispetto al sistema di riferimento ![]() si ottiene studiando le componenti del moto lungo l’asse
si ottiene studiando le componenti del moto lungo l’asse ![]() e lungo l’asse
e lungo l’asse ![]() .
.
Per ![]() ,
, ![]() e
e ![]() .
.
(1) ![]()
(2) ![]()
Sostituendo nella (2) ![]() ricavata dalla (1), si ottiene l’equazione della traiettoria:
ricavata dalla (1), si ottiene l’equazione della traiettoria:
![]()
e sostituendo i valori noti di ![]() e di
e di ![]() :
:
(3) 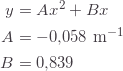
(con ![]() e
e ![]() in metri). Si tratta di una parabola, passante per l’origine e con la concavità verso il basso (vedi figura).
in metri). Si tratta di una parabola, passante per l’origine e con la concavità verso il basso (vedi figura).
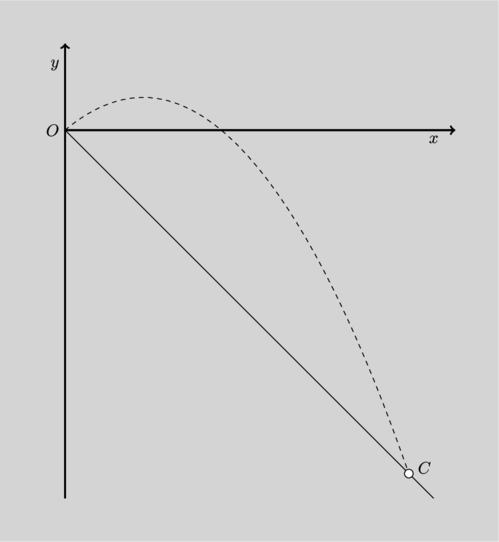
b) Il punto ![]() è una delle due intersezione della parabola (3) con la retta passante per
è una delle due intersezione della parabola (3) con la retta passante per ![]() e per
e per ![]() di equazione
di equazione ![]() .
.
Si tratta, quindi, di risolvere il sistema tra questa equazione e la (3). Confrontando tra loro le due equazioni, si ottiene:
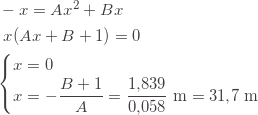
In corrispondenza al valore ![]() , si ha:
, si ha: ![]() .
.
Da ultimo si può calcolare: ![]() .
.
c) Per calcolare la durata del salto da ![]() a
a ![]() , basta considerare la componente orizzontale del moto descritta dalla (1). Si ha:
, basta considerare la componente orizzontale del moto descritta dalla (1). Si ha:
![]() .
.
I dati di questo problema sono realistici?
In verità no. Uno sciatore che atterrasse come previsto nello schema ora presentato avrebbe una velocità di circa di ![]() e soprattutto, un angolo di impatto troppo alto. L’urto sul terreno sarebbe confrontabile con quello di un salto diretto da un’altezza di un po’ più di
e soprattutto, un angolo di impatto troppo alto. L’urto sul terreno sarebbe confrontabile con quello di un salto diretto da un’altezza di un po’ più di ![]() .
.
Come avviene allora che nei salti dal trampolino si realizzano distanze di volo molto più grandi di quella qui calcolata?
La differenza principale sta nel fatto che l’angolo di distacco (pressoché orizzontale) e la forma del pendio sono disegnati in modo che l’atterraggio avvenga con un angolo molto piccolo rispetto al suolo. Inoltre i saltatori “veleggiano” nell’aria prima di concludere il salto.
Per curiosità, potete guardare lo schema del trampolino olimpico di Garmish-Partenkirchen, in Baviera.